Elaborazione digitale di immagini

26 Febbraio 2013

1-Immagini digitali

Un'immagine digitale in bianco nero può essere descritta da una matrice $m\times n$ di pixel (contrazione di picture element). Il generico pixel $p(i,j)$, il cui valore numerico può essere intero o reale, fornisce la luminosità del punto di coordinate $(i,j)$ dell'immagine.

Formato PGM (Portable Gray Map). Nella convenzione PGM il file che contiene le informazioni sull'immagine è organizzato nel modo seguente:

P2
# eventuali commenti
numero_colonne, numero_righe
valore_livello_bianco
p(1,1)
p(1,2)
.
.
p(1,n)
p(2,1)
p(2,2)
.
.
 

dove:
P2, detto numero magico, indica al sistema che visualizzerà il file sullo schermo che si tratta di una immagine bianco nero nel formato PGM
# eventuali commenti  sono commenti arbitrari preceduti da #
numero_colonne e numero_righe sono due interi che determinano le dimensioni dell'immagine (matrice dei pixel)
valore_livello_bianco è un intero compreso tra 1 e 65536, che determina il valore numerico del bianco (generalmente 255), mentre il valore numerico del nero è 0.
p(i,j) sono i valori numerici dei pixel (fra 0 e valore_livello_bianco) relativi alla posizione $(i,j)$. Essi sono ordinati per righe.

Maggiori informazioni si trovano nel sito netpbm.sourceforge.net

Esistono diversi programmi per visualizzare un'immagine sullo schermo di un computer, il più semplice è display. Un pacchetto che permette di fare elaborazioni varie oltre che visualizzare una immagine è gimp.
Ad esempio, se immagine.pgm è il nome di un file che contiene un'immagine codificata nel formato PGM, allora il comando

mostra sullo schermo l'immagine corrispondente al file, mentre il comando

gimp immagine.pgm

lancia l'applicazione gimp visualizzando sullo schermo il contenuto di immagine.pgm.

Esempio di file PGM

P2
# esempio semplice
4,4
255
0
0
0
0
0
255
255
0
0
255
255
0
0
0
0
0

La stessa immagine poteva essere memorizzata come

P2
# esempio semplice
4,4
255
0   0   0   0
0 255 255   0
0 255 255   0
0   0   0   0

File ASCII e file RAW
Un file PGM può essere memorizzato nella modalità ASCII o nella modalità RAW.
Nella modalità ASCII il valore del generico pixel viene scritto nella sua rappresentazione decimale con caratteri ASCII. Ad esempio. se il valore del pixel è 123, vengono scritte le tre cifre 1,2 e 3, consumando quindi tre byte di memoria, uno per ciascuna cifra, più altri tre byte per gli spazi di separazione. Nella rappresentazione RAW, il pixel il cui valore è 123 viene memorizzato con il singolo byte il cui valore è 123. In questo modo un solo byte è sufficiente per ciascun pixel. Nella rappresentazione RAW la stringa P2 va sostituita con P5. La rappresentazione ASCII è più comoda perché permette di essere visualizzata e manipolata più facilmente. Ha lo svantaggio che è più ingombrante. Noi useremo la rappresentazione ASCII.

Un altro modo di convertire immagini da un formato ad un altro è dato dal comando convert presente in tutte le distribuzioni di linux. Ad esempio,

convert foto.jpg foto.pgm

trasforma il file foto.jpg, contenente una fotografia nel formato jpeg, nel file foto.pgm contenente la stessa immagine ma in b/n nel formato pgm.

Formato PBM (Portable Bit Map). È un formato analogo al PGM dove il numero magico è P1 in modalità ASCII e P4 in modalità raw, e dove i pixel possono assumere solo due valori 0 e 1 (nero e bianco). Manca quindi il valore della massima intensità del bianco.

Immagini a colori, modalità RGB --- Formato PPM
Una immagine a colori può essere memorizzata mediante la modalità RGB (Red, Green, Blue). In questo modo ad ogni pixel viene assegnata una terna di numeri $r,g,b$, dove $r$ fornisce l'intensità del rosso, $g$ l'intensità del verde e $b$ l'intensità del blu. Il file che viene costruito nel formato PPM (Portable Pixel Map) è organizzato come segue

P3
# eventuali commenti
numero_colonne, numero_righe
massima_luminosità
r(1,1)   g(1,1)   b(1,1)
r(1,2)   g(1,2)   b(1,2)
.
.
.

Ciò che cambia rispetto ad un file b/n è la prima riga che contiene P3 a indicare che è un file a colori nella modalità RGB e la presenza delle terne di pixel (un valore numerico per ogni colore) anziché dei singoli valori. Le terne dei valori rgb possono non stare sulla stessa riga ma essere distribuite su righe consecutive. Nella codifica RAW la stringa P3 viene sostituita da P6.

Maggior dettagli si trovano a netpbm.sourceforge.net

Il formato PNM, acronimo di Portable aNy Map, è giusto un'astrazione dei formati PBM, PGM, and PPM. Cioè il termine PNM si riferisce collettivamente a PBM, PGM, e PPM.

Immagini in octave

Il linguaggio di programmazione Octave permette in modo semplice di trasformare una matrice di numeri in una immagine usando una logica simile a quella dello standard pnm. Octave usa una mappa dei colori che è costituita da una matrice di $k$ righe e tre colonne. Per default $k=64$. Gli elementi di questa matrice sono numeri compresi tra 0 e 1, ciascuna riga rappresenta un colore composto da quantità di rosso, verde e blu date dai valori presenti rispettivamente sulla prima, seconda e terza colonna. Ad esempio una mappa del tipo
[1 0 0; 0 1 0; 0 0 1]
fornisce tre colori, nell'ordine: il rosso, il verde e il blu. Per default la mappa dei colori contiene 64 tonalità di colore. Per creare una mappa di grigi basta assegnare uguali quantità di rosso, verde e blu a ciascun colore. Una mappa di 64 livelli di grigio ha quindi per colonne [0:1/63:1]'*[1 1 1].

Per poter cambiare la mappa dei colori basta dare il comando
colormap(nuovamappa);
dove nuovamappa è la matrice con la nuova mappa dei colori.
Ad esempio per creare una mappa MP che abbia i soli tre colori puri rosso, verde e blu basta scrivere
MP=eye(3); colormap(MP);
Per tornare alla mappa default di 64 colori basta scrivere
colormap('default');
Per assegnare la mappa di colori corrente ad una matrice CM basta scrivere
CM = colormap;

Per poter visualizzare un'immagine in octave ci sono diversi modi. Essi differiscono leggermente tra loro a seconda della versione di Octave usata. Sulle macchine dell'aula M c'è la versione 2.9.19. Sulle macchine dell'aula 4 del dipartimento di matematica c'è la versione 3.0.5. Si suggerisce l'uso del comando "help" per avere informazioni sulla sintassi e sul funzionamento di un qualsiasi comando Octave. Qui descriviamo i comandi nella versione 3.0.5.

Il comando image
Se la variabile A contiene una matrice di $m$ righe e $n$ colonne con valori numerici A(i,j), il comando
image(A);
mostra sullo schermo una immagine formata da $m\times n$ pixel dove la luminosità e il colore del pixel di posizione (i,j) sono determinati dal valore di A(i,j); più precisamente il colore del pixel di posto $i,j$ è dato dal colore della mappa dei colori presente sulla $q$-esima riga di mappa dove $q$ è l'arrotondamento alla parte intera di A(i,j). Valori di A(i,j) fuori dal segmento consentito corrispondono al primo e all'ultimo colore della mappa a seconda della parte del segmento in cui cade A(i,j).
Nello stesso comando si possono specificare gli estremi dell'asse x e dell'asse y in modo che nell'immagine compaiano le coordinate. Per far questo si usa image con la sintassi
image([xmin xmax], [ymin ymax], A);
Ad esempio, il comando
colormap(eye(3));
A=[-1 0 1 2 3 4 ; -1 0 1 2 3 4];
image([-1 4], [0 1], A);
genera l'immagine


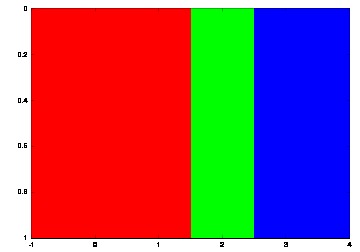
Si noti che tutti i valori degli elementi di A minori di 1/2 corrispondono al colore rosso (il primo della mappa dei colori) mentre i valori maggiori o uguali a a 2.5 corrispondono al colore blu (il terzo della mappa dei colori).
Il comando image può prendere in input una matrice $m\times n\times 3$. In questo caso l'immagine mostrata sullo schermo dipende dal numero di colori presenti nella mappa ma è indipendente dalla particolare mappa dei colori al momento in uso. I valori del rosso, verde e blu sono dati dai valori numerici delle tre matrici A(:,:,1), A(:,:,2), A(:,:,3). I valori minori o uguali a 0 corrispondono ad assenza di colore, i valori maggiori o uguali a $c$ corrispondono alla massima luminosità, dove $c$ è il massimo numero di colori nella mappa corrente. Ad esempio avendo in uso la mappa default con 64 colori, i comandi
r=zeros(6); g=zeros(6); b=zeros(6);
r(:,1:4)=64; g(:,3:6)=64; b(1:3,:)=64;
A(:,:,1)=r; A(:,:,2)=g; A(:,:,3)=b;
image(A);

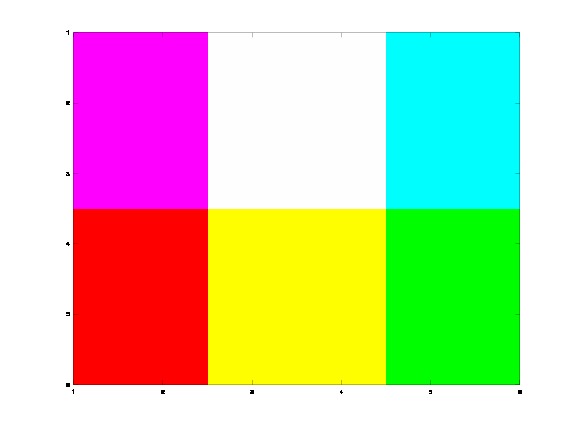
Il comando imagesc
Il comando imagesc(A) ha lo stesso effetto e la stessa sintassi di image. L'unica differenza è che gli elementi della matrice A vengono scalati in modo che il minimo e il massimo corrispondano al minimo e massimo indice della mappa dei colori. Se $A$ è $m\times n\times 2$ allora i valori degli elementi di A vengono scalati in modo da rientrare nel segmento [0 64].
Apparentemente nella versione 2.9.19 di Octave non ci sono differenze di comportamento tra i comandi image e imagesc.

Esempio 1. Il comando imshow(rand(20,20,3)); visualizza una immagine a colori $20\times 20$ i cui pixel hanno una quantità casuale di rosso, verde e blu. Un'immagine analoga si ottiene col comando image(rand(20,20,3));

Il programma Octave seguente costruisce un'immagine n×n con valori di grigio che sfumano da nero a bianco secondo la regola A(i,j)=i+j, e dove 2 corrisponde a nero e 2n a bianco.

function grigi (n)
  a = zeros(n);
  for i = 1 : n
    for j = 1 : n
      a(i,j) = i + j;
    endfor
  endfor
  colormap([0:1/63:1]'*[1 1 1]);
  imagesc(a);
endfunction

L'immagine che si ottiene in questo modo è la seguente:

Provate a lanciare il gomando grigi(100) e poi guardate come cambia la figura col comando
mappa=rand(200,3);colormap(mappa);
Provate ancora a sostituire l'istruzione
a(i,j) = i + j;
con l'istruzione
a(i,j) = i * j;
e ancora guardate come cambia l'immagine col comando colormap(mappa);. Provate separatamente queste altre scelte e motivate la variazione dell'immagine
a(i,j) = (i + j)*rand;
a(i,j) = i*j*rand;

Osserviamo che la costruzione col doppio ciclo for per assegnare i valori i+j, oppure i*j alla matrice a può essere sostituita dai comandi più semplici e più efficienti
a=[1:n]'*ones(1,n)+ones(n,1)*[1:n];
e, rispettivamente
a=[1:n]'*[1:n];

Osserviamo che la function grigi permette di tracciare le linee di livello della funzione che abbiamo assegnato alla matrice a(i,j). Proviamo ad esempio a considerare la funzione $\cos(x)\cos(y)$ per $x$ e $y$ compresi tra zero e pigreco. Poniamo allora
a(i,j) = cos(pi*i/n)*cos(pi*j/n);
lanciamo grigi(200); e poi mappa=rand(10,3);colormap(mappa); In questo modo vengono evidenziate 10 linee di livello.

Se vogliamo creare un file che contiene i dati di questa immagine nel formato pgm basta inserire nella function precedente i seguenti comandi:

 fid = fopen('grigi.pgm', 'w');
 fprintf(fid,'P2\n');
 fprintf(fid, '%d , %d \n', n, n);
 fprintf(fid, '255\n');
 for i = 1 : n
   for j = 1 : n
     fprintf(fid, '%d\n', a(i,j) );
   endfor
 endfor

Il comando fopen di Octave apre un file per la lettura/scrittura la sintassi è fid=fopen(nomefile, modo) dove nomefile è una stringa col nome del file che si vuole aprire, modo è una stringa che contiene la modalità di apertura, in particolare:

'w' write (file di scrittura)
'r' read (file di lettura)

la variabile fid prende come valore un numero intero che servirà a identificare il file di lettura/scrittura. Infatti, l'istruzione

fprintf(fid, 'scrivo %d', n);

scrive il valore intero della variabile n preceduto dalla parola scrivo. La sintassi per i formati di scrittura è la stessa del linguaggio C.

1.1-Immagini create dai numeri primi: la spirale di Ulam

Immagini interessanti possono essere costruite per evidenziare proprietà dei numeri primi

Esempio 2. Costruiamo una immagine $n\times n$ tale che il pixel di posto $(i,j)$ sia bianco se $n(i-1)+j$ è un numero primo, sia nero altrimenti. Per questo ci occorre una funzione che dato un intero $p$ ci dice se $p$ è primo o no.

function evidenzia_primi(n)
  imag = zeros(n);
  for i = 1 : n
    for j = 1 : n
      imag(i,j)=primo(n*(i-1)+j);
    endfor
  endfor
  imagesc(imag);
endfunction

function v = primo(p)
  v=1;
  for i = 2 : sqrt(p)
    if mod(p,i)==0
      v = 0;
      break;
    endif
  endfor
endfunction

La figura che si ottiene con $n=100$ è la seguente


Esaminate le tre immagini che si ottengono con $n=119$, $n=120$, $n=121$. Sapete spiegare il perché di quelle configurazioni particolari?

Un pochino più complicato, ma vale la pena farlo, è numerare i pixel lungo una spirale che si dipana dal centro del quadrato, partendo dal numero 1

e accendere i pixel che corrispondono ai numeri primi. In questo modo si ottiene la spirale di Ulam.

Osservate che i numeri primi sembrano addensarsi maggiormente lungo delle rette inclinate di un angolo di 45 gradi. È questo un effetto ottico o è qualcosa che evidenzia una qualche proprietà nascosta? Una discussione su questa domanda si può trovare su Wikipedia http://en.wikipedia.org/wiki/Ulam_spiral

Per realizzare questa immagine ci costruiamo prima una function che dispone i numeri naturali in una matrice $(2m+1)\times(2m+1)$ partendo dal centro, cioè dall'elemento di posto $(m,m)$ e muovendosi a spirale che si dipana in senso antiorario compiendo $m$ giri.
Per capire come procedere facciamo riferimento alla seguente figura

Si è colorato il primo giro di giallo, il secondo di rosa e il terzo di oro. Ciascun giro è ripartito in quattro tratti: un tratto a salire, uno di movimento a sinistra, uno a scendere ed uno di movimento a destra.
La function che fa questo è descritta di seguito:

function s = spirale(m)
% Costruisce la matrice s di dimensione 2m+1 che contiene i
% numeri interi positivi a partire dal centro a spirale antioraria
   s = zeros(2*m+1);
   i = m+1; j=m+1;
   k = 1;
   s(i,j) = k;
   for giri = 1:m % conta i giri della spirale
     k = k+1;
     j = j+1;
     s(i,j)=k;
     for t = 1:2*giri-1 % sale
       k = k+1;
       i = i-1;
       s(i,j) = k;
     endfor

     for t = 1:2*giri % sinistra
       k = k+1;
       j = j-1;
       s(i,j) = k;
     endfor

     for t = 1:2*giri % basso
       k = k+1;
       i = i+1;
       s(i,j) = k;
     endfor

     for t = 1:2*giri % destra
       k = k+1;
       j = j+1;
       s(i,j) = k;
     endfor
   endfor
endfunction

I quattro tratti in cui abbiamo spezzato la numerazione degli interi lungo la spirale sono evidenziati con commenti nel programma. Osservate che la variabile giri conta i giri della spirale intorno al suo centro, e per ciascun giro si percorrono i quattro lati. La variabile k contiene il valore dell'intero da depositare nella casella corrente della spirale.

Un programma che genera la spirale di Ulam è il seguente

function a = spirale_di_ulam(m)
  a = zeros(2*m + 1);
  s = spirale(m);
  for i = 1 : 2*m + 1
    for j = 1 : 2*m + 1
      if primo(s(i,j))
        a(i,j) = 1;
      endif
    endfor
  endfor
endfunction

Il linguaggio Octave, essendo interpretato, ha tempi di elaborazione molto elevati. In particolar modo questo succede in presenza di cicli for annidati. Usando i programmi scritti sopra siamo in grado di trattare dimensioni relativamente basse e quindi possiamo creare solo immagini piccole. Per poter svolgere elaborazioni a dimensione più ampia occorre implementare questi algoritmi con linguaggi più efficienti tipo il linguaggio C o il Fortran 90. Una alternativa possibile è usare ancora Octave evitando però di usare cicli for annidati e utilizzando il più possibile istruzioni "vettoriali", cioè istruzioni che anziché operare sulle singole componenti di un vettore o di una matrice agiscono simultaneamente su porzioni del vettore o della matrice stessa. Mostriamo un esempio di ciò nell'implementazione del crivello di Eratostene.

Crivello di Eratostene. Il crivello di Eratostene è un metodo per selezionare i numeri primi compresi tra 1 ed $n$, dove $n$ è un intero positivo assegnato. Il metodo funziona così: dalla lista degli interi da 1 a $n$ si toglie il numero 1, poi tutti i multipli interi di 2, escluso naturalmente 2, poi tutti i multipli interi di 3 escludendo 3, e così via fino ad arrivare a togliere i multipli del più grande intero minore o uguale alla radice quadrata di $n$. Alla fine rimangono i numeri primi. Questo metodo può essere implementato partendo dal vettore di tutti uni e azzerando le componenti che hanno indice non primo in modo che alla fine il vettore ottenuto conterrà il valore 1 in corrispondenza delle componenti di indice primo e zero altrimenti. Di questo metodo proponiamo due implementazioni una di tipo sequenziale che usa cicli for, e quindi più lenta, e l'altra di tipo vettoriale e quindi più veloce.

function primi=crivello0(n)
% Calcola i numeri primi da 1 a n col crivello di Eratostene
% versione sequenziale
  primi=ones(1,n);
  primi(1)=0;
  m=round(sqrt(n));
  for i=2:m
    for j=2:n/i
      primi(i*j)=0;
    endfor
  endfor
endfunction

function primi = crivello(n)
% Calcola i numeri primi da 1 a n col crivello di Eratostene
% versione vettoriale
  primi = ones(1,n);
  m=round(sqrt(n));
  primi(1) = 0;
  for i = 2:m
    primi(2*i:i:n) = 0;
  endfor
endfunction

La spirale di Ulam può essere generata in modo più efficiente in questo modo

function z = ulam(n)
% Disegna la spirale di Ulam di dimenione 2n+1
% e fornisce in uscita la matrice relativa
   s = spirale(n);
   m = max(max(s));
   c = crivello(m);
   z = c(s);
   imagesc(z);
endfunction

Una caratteristica importante di Octave è data dall'istruzione z=c(s); in cui viene fornita in uscita la matrice il cui elemento di posto $(i,j)$ è dato da $c(s(i,j))$. Cioè il vettore $c$, inteso come funzione definita sull'insieme $\{1,2,...,m\}$ a valori in $\{0,1\}$, viene composto con la matrice $s$ intesa come applicazione definita su $\{1,2...,2n+1\}\times\{1,2,...,2n+1\}$ a valori in $\{1,2,...,m\}$.

Esercizio 1. Dare una versione vettoriale, basata sul crivello di Eratostene, del programma che crea un'immagine in cui il pixel di posto $(i,j)$ è bianco se il numero $n(i-1)+j$ è primo, altrimenti è nero. [Aiuto: costruire una matrice $S$ il cui elemento di posto $(i,j)$ è $j+ n(i-1)$ e calcolare $c(S)$ dove $c$ è il vettore dato dal crivello di Eratostene. Per calcolare $S$ si scriva $S$ come somma $P+Q$ dove $P=$ones(n,1)*[1:n]; e $Q$ è data da ....]

Esercizio 2. Evidenziare le coppie di numeri interi $(p,q)$ tali che $p^2+q^2$ è un numero primo. Per questo create una immagine di dimensione $n\times n$ in cui il pixel di posto $(p,q)$ è bianco se $p^2+q^2$ è primo, nero altrimenti. Dare anche una versione vettoriale del programma. [Aiuto: per la versione vettoriale costruire una matrice $S$ che abbia nel posto $(p,q)$ l'elemento $p^2+q^2$ e si calcoli $c(S)$. Per il calcolo di $S$ si proceda come nell'esercizio 1]

Esercizio 3. Evidenziare le coppie di numeri interi $(p,q)$ tali che $|p^2-q^2|+k$ è un numero primo. Per questo create una immagine di dimensione $n\times n$ in cui il pixel di posto $(p,q)$ è bianco se $|p^2-q^2|+k$ è primo, nero altrimenti, dove $k=1$, $k=2$, $k=3$. Dare anche una versione vettoriale del programma.

Esercizio 4. Evidenziare le coppie di numeri interi $(p,q)$ tali che $|p^2-q^2|+k$ è un numero primo sia per $k=1$ che per $k=3$. Per questo create una immagine di dimensione $n\times n$ in cui il pixel di posto $(p,q)$ è bianco se $|p^2-q^2|+k$ è primo, sia per $k=1$ che per $k=3$, è nero altrimenti. Dare anche una versione vettoriale del programma.

Esercizio 5. Evidenziare le coppie di numeri interi $(p,q)$ tali che $pq+1$ è un numero primo. Per questo create una immagine di dimensione $(2m+1)\times(2m+1)$, dove $m$ è un intero assegnato ad esempio $m=100$, e accendete il pixel in posizione $(i,j)$ se $|(i-m)(j-m)|+1$ è primo. In quest'ultimo caso si ottiene
 

Guardando attentamente questa immagine si riescono a evidenziare particolari forme geometriche.

Esercizio 6. Evidenziare le coppie $(p,q)$ di numeri primi consecutivi (primi gemelli) usando la spirale di Ulam, colorando di rosso i numeri primi gemelli e di verde gli altri numeri primi.

Esercizio 7. Numerare gli elementi di una matrice a partire da quello in posizione (1,1) e procedendo a zig-zag: (1,1), (1,2), (2,1), (3,1), (2,2), (1,3), (1,4), (2,3), (3,2), (4,1), ... ed accendere i pixel di un'immagine relativi alle coppie $(i,j)$ che corrispondono a numeri primi.

Esercizio 8. Studiare graficamente come sono distribuiti i numeri primi della forma $pq+p+q+k$ con $k=0,1,2,3,4$.

1.2- Bacini di attrazione

Talvolta è utile studiare la dinamica delle successioni generate da espressioni del tipo \[ z_{k+1} = g(z_k) \] al variare del valore iniziale $z_0$. Questo capita ad esempio quando la successione viene costruita per calcolare i punti fissi della funzione $g(x)$ definita sul piano complesso. Un esempio classico è dato dal metodo di Newton applicato all'equazione $x^3 - 1 = 0$ che fornisce l'iterazione \[ z_{k+1}=z_k-(z_k^3-1)/(3z_k^2) \] Le successioni generate in questo modo possono convergere a ciascuno dei tre zeri del polinomio $x^3-1$ o possono divergere. È allora interessante individuare per quali valori di $z_0$ la successione converge a 1, per quali valori la successione converge a $-1/2 + {\bf i} \sqrt 3/2$ e per quali valori la successione converge a $-1/2 -{\bf i} \sqrt 3/2$, dove $\bf i$ è l'unità immaginaria.
Si riportano qui sotto gli zeri del polinomio $x^3-1$.

Proviamo a creare una immagine che rappresenti una porzione del piano complesso, ad esempio di centro 0 e semilato 1, in cui il generico pixel viene colorato di rosso se il corrispondente numero complesso assegnato a $z_0$ genera una successione che converge a 1, di verde se la successione converge a $-1/2+{\bf i} \sqrt 3/2$, di blu se converge a $-1/2-{\bf i}\sqrt 3/2$ e di nero se la successione non converge. Naturalmente dobbiamo dare un numero massimo di passi oltre il quale si assume che non ci sia convergenza se il valore corrente $x_k$ non si trova in un intorno sufficientemente piccolo di uno degli zeri.
Procediamo inizialmente nel modo seguente per creare una immagine di $(2m+1)\times(2m+1)$ punti, dove $m$ è un intero assegnato.
Poniamo $h=1/m$ e consideriamo una griglia di $(2m+1)\times(2m+1)$ punti $w_{i,j}$ nel quadrato $[-1,1]\times[-1,1]$ del piano complesso definiti da $w_{i,j} =(j+{\bf i}i)h$, $i=-m,m$, $j=-m,m$.

function a = newton(m)
  maxit = 20;
% zeri del polinomio
  x1 = 1;
  x2 = -0.5+I*sqrt(3)/2;
  x3 = -0.5-I*sqrt(3)/2;
  a = 4*ones(2*m+1);
  h = 1/m;
  for i = -m : m
    for j = -m:m
      z = (j+i*I)*h;
% itera
      for k = 1 : maxit
        z = g(z);
      endfor
% colora
      if abs(z-x1)<1.0e-4
        a(m+i+1,m+j+1) = 1;
      endif
      if abs(z-x2)<1.0e-4
        a(m+i+1,m+j+1) = 2;
      endif
      if abs(z-x3)<1.0e-4
        a(m+i+1,m+j+1) = 3;
      endif
    endfor
  endfor
  mappa = [1 0 0; 0 1 0; 0 0 1; 0 0 0];
  colormap(mappa);
  imshow(a,mappa);
endfunction

function y = g(z)
  y = 0;
  if z!=0
    y = z - (z^3 - 1)/(3*z^2);
  endif
endfunction

function a = newton1(m)
% zeri del polinomio
  x1 = 1;
  x2 = -0.5+I*sqrt(3)/2;
  x3 = -0.5-I*sqrt(3)/2;
  maxit = 20;
  range = -2:2/m:2;
  n = 2*m+1;
  z = ones(n,1)*range + I*range'*ones(1,n);
% itera simultaneamente su tutti i punti
    z = z + 1.e-16; % per evitare lo zero
  for k = 1 : maxit
    y = z.*z;
    zz = z - (z.*y - ones(n))./(3*y);
  endfor
  b = zeros(3,n,n);
  b(1,:,:) = z-x1; % sottrae x1 a tutte le componenti di z
  b(2,:,:) = z-x2; % sottrae x2 a tutte le componenti di z
  b(3,:,:) = z-x3; % sottrae x3 a tutte le componenti di z
  [valori, posizioni] = min(abs(b));
  a = reshape(posizioni, [n n]); %
endfunction

Esercizio 1. Si modifichi la function newton1 in modo da prendere in input, oltre che alla dimensione $m$, il centro $c$ (numero complesso) e il semilato $L$ in modo che venga rappresentata nell'immagine la porzione di piano racchiusa dal quadrato centrato in $c$ e di semilato $L$.

Esercizio 2. Si modifichi la function newton1 in modo da colorare i pixel in base al minimo numero di passi sufficienti affinché $|z_k - z_{k-1}|\lt 1/10000$, indipendentemente dal valore del limite.
[Aiuto: siano Z e W le matrici col valore corrente e il valore successivo al generico passo dell'iterazione; si consideri la matrice H=abs(W-Z) > 1.0e-4 che in posizione $(i,j)$ contiene 1 se la componente di posto $(i,j)$ di abs(W-Z) è maggiore di 1.0e-4, contiene zero altrimenti; si accumuli in una variabile S la somma delle H]

Esercizio 3. Scrivere una function vettorizzata che crea immagine con colori rosso, verde e blu di diversa intensità in base al numero di iterazioni, dove il colore è scelto in base al valore del limite della successione generata.

Esercizio 4. Creare una analoga function che crea un file PNM corrispondente all'immagine dell'esercizio precedente.
Si dia una colorazione ancora diversa assegnando la quantità r,g,b di rosso, verde e blu in funzione del numero di iterazioni mediante tre funzioni diverse, ad esempio $r=1231 k$ mod $256$, $g=2753 k$ mod $256$, $b=3127 k$ mod $256$.

Esercizio 5. Si creino i bacini di attrazione per il metodo di Newton applicato alle tre equazioni equivalenti:
$x^2 - x^{-1} = 0$,
$x - x^{-2} = 0$,
$1 - x^{-3} = 0$.

Ecco alcune immagini così ottenute

Equazione $x^3-1=0$

Equazione $x^2-x^{-1}=0$

Equazione $x-x^{-2}=0$

Equazione $1-x^{-3}=0$

È possibile creare dei filmati come il seguente che traccia i bacini di attrazione del metodo di Newton applicato all'equazione $x^p-1=0$ con $p$ che varia tra 3 e 4. Il filmato è stato creato da uno studente del corso a.a. 2008-2009.

Esercizio 6. Si consideri il polinomio $1000x^4-10000x^3-x+1$ che ha tre zeri di modulo 1/10 e uno zero uguale ad 1. Si costruiscano le immagini relative ai bacini di attrazione del metodo di Newton applicato alle funzioni
$1000x^4-10000x^3-x+1$
$1000x^3-10000x^2-1+x^{-1}$
$1000x^2-10000x-x^{-1}+x^{-2}$
$1000x-10000-x^{-2}+x^{-3}$
$1000-10000x^{-1}-x^{-3}+x^{-4}$

1.3- L'insieme di Mandelbrot e gli insiemi di Julia

Esercizio 7. Si scriva una function in Octave che disegna la porzione della figura di Mandelbrot in un quadrato di centro e semilato assegnati nel seguente modo: si svolgono $q=50$ iterazioni e per ogni coppia $(i,j)$ si calcola il numero di passi $k$ che occorrono affinché $z_k$ abbia modulo maggiore di 2; si colora il pixel di posto $(i,j)$ col $k$-esimo colore della tavola dei colori; se dopo $q$ iterazioni il modulo di $x_q$ è minore di 2 si colora il pixel $(i,j)$ col colore $q$-esimo della tavola dei colori. Dare una versione vettorizzata della function.

Fissato un valore di $c$, l'insieme dei punti $z_0$ tali che la successione $z_k$ non diverge è chiamato insieme di Julia.

Esercizio 8. Si scriva una function in Octave che, dato $c$, traccia l'insieme di Julia relativo ad una porzione del piano di centro e semilato assegnati. Dare una versione vettorizzata della function.

Compito 1 Esercizio 7
Compito 2 Esercizio 8
Compito 3 Il polinomio $p(x)=x^5-(100x-1)^3$ ha tre radici molto vicine a 1/100. Scrivere una function che traccia i bacini di attrazione del metodo di Newton applicato all'equazione $p(x)=0$ nel quadrato di centro $1/100$ e semilato $d$. Trovare valori sufficientemente piccoli di d che evidenzino i tre bacini di attrazione. Spedire il valore di $d$ e la function.
Compito 4 Svolgere il compito 3 con la funzione $p(x)=x^2-(100-1/x)^3$.
Compito 5 Svolgere il compito 3 con la funzione $p(x)=1-x^{-2}(100-1/x)^3$.
Compito 6 Svolgere il compito 3 con la funzione $p(x)=x-x^{-1}(100-1/x)^3$.
Compito 7 Svolgere il compito 3 con la funzione $p(x)=x^4-x^{-1}(100x-1)^3$.
Compito 8 Svolgere il compito 3 con la funzione $p(x)=x^3-x^{-2}(100x-1)^3$.

2-Manipolazioni geometriche.
È possibile ruotare una immagine attorno al pixel di coordinate $(i_0,j_0)$ di un angolo $\alpha$ in senso antiorario semplicemente applicando una rotazione alle coordinate di ciascun pixel. Prima di vedere questo, osserviamo che nella nostra notazione "matriciale" la coppia $(i,j)$ denota l'elemento della riga $i$ e della colonna $j$, per cui è come avere messo l'origine degli assi nell'angolo in alto a sinistra dell'immagine col primo asse che punta verso il basso e il secondo che punta a destra. Detto questo, ricordiamo che le coordinate del punto $P'=(x',y')$ ottenuto ruotando attorno a $(x_0,y_0)$ di un angolo $\alpha$ in senso antiorario il punto $P$ di coordinate $(x,y)$ sono \[\begin{array}{l} x' - x_0 = (x-x_0)\cos(\alpha) - (y-y_0)\sin(\alpha)\\ y' - y_0 = (x-x_0)\sin(\alpha) + (y-y_0)\cos(\alpha) \end{array} \] Quindi, si ottiene \[\begin{array}{l} i' - i_0 = (i-i_0)\cos(\alpha) - (j-j_0)\sin(\alpha)\\ j' - j_0 = (i-i_0)\sin(\alpha) + (j-j_0)\cos(\alpha) \end{array} \] Osserviamo che se $(i,j)$ è una coppia di interi non è detto che $(i',j')$ sia ancora una coppia di interi.

Per meglio descrivere la function di rotazione denotiamo con $A=(a_{i,j})$ la matrice corrispondente all'immagine di partenza, e con $B=(b_{i,j})$ la matrice corrispondente all'immagine ruotata. Allora, per eseguire la rotazione in modo più efficace, scandiamo tutte le coppie intere $(i',j')$ corrispondenti ai pixel del supporto dell'immagine ruotata, applichiamo la trasformazione inversa ottenendo la coppia $(i,j)$, non necessariamente intera, e andiamo a riempire l'elemento $b_{i',j'}$ col valore di $a_{[i],[j]}$, dove $[i]$ e $[j]$ denotano gli arrotondamenti di $i$ e $j$ alla parte intera. Può accadere che la coppia $([i],[j])$ non stia nel supporto dell'immagine, cioè che $[i]$ non sia compreso tra $1$ e $n$, e $[j]$ non sia compreso tra $1$ e $m$. In tal caso assegnamo a $b_{i',j'}$ il valore $0$.

Scriviamoci qui sotto le formule inverse della rotazione cioè \[\begin{array}{l} i - i_0 = (i'-i_0)\cos(\alpha) + (j'-j_0)\sin(\alpha)\\ j - j_0 = -(i'-i_0)\sin(\alpha) + (j'-j_0)\cos(\alpha) \end{array} \] Il programma che realizza questa trasformazione è il seguente dove abbiamo usato le variabili ip,jp per denotare $i'$ e $j'$.

function y = ruota(x, p, ang)
%  ruota un'immagine data dalla matrice x attorno al pixel p di un angolo ang in senso antiorario
   m = size(x)(1);
   n = size(x)(2);
   i0 = p(1); j0 = p(2);
   for ip = 1 :  m
      for jp = 1  : n                                       %   seleziona il pixel di posizione (ip,jp) dell'immagine ruotata
          i = round(i0+(ip-i0)*cos(ang)+(jp-j0)*sin(ang));  %   calcola il pixel di posizione (i,j) dell'immagine di provenienza
          j = round(j0-(ip-i0)*sin(ang)+(jp-j0)*cos(ang));
          if(i>0  &&  i<=m  &&  j>0  && j<=n)               %   se il pixel di provenienza sta nel supporto dell'immagine
               y(ip,jp) = x(i,j);                           %   prende il valore dell'immagine
         else
               y(ip,jp) = 0;                                %   altrimenti prende il valore nullo (nero)
            endif
        endfor
    endfor
endfunction

Ecco il risultato che si ottiene con angolo = 1 radiante

a partire da un'immagine originale di cammelli
 

Sapreste deformare l'immagine in modo che l'angolo di rotazione sia inversamente proporzionale alla distanza del pixel dal centro dell'immagine di coordinate $(i_0,j_0)$? Per questo basta cambiare  la parte in cui si calcolano $i$ e $j$ ad esempio con
        s = sqrt((i0-ip)^2 + (j0-jp)^2))/10 + 0.01;
        a = 6.28/s;
        i = i0 + (ip-i0)*cos(a) + (jp-j0)*sin(a);
        j = j0 - (ip-i0)*sin(a) + (jp-j0)*cos(a);

Il numero 0.01 che è stato aggiunto alla variabile s, serve per evitare situazioni di singolarità nel centro di rotazione. Ecco il risultato che si ottiene

Una semplice function che legge i dati da un file pgm o ppm e li assegna ad una matrice è riportata di seguito

function a= leggifoto(nome)
% A = leggifoto("nomefile");
% legge un file pgm o ppm e mette i valori in A
% A ha dimensione mxn se il file e' pgm
% A ha dimensione mxnx3 se il file e' ppm
% il file deve essere di tipo ASCII e non deve avere commenti
    fid = fopen (nome, "r");
    p=fgetl (fid, 2);
    [v,l]=fscanf(fid,"%d");
    m=v(2);n=v(1);
    if p=="P2"
       a=reshape(v(4:m*n+3),n,m)';
    elseif p=="P3"
       c=reshape(v(4:m*n*3+3),3,n,m);
       a=zeros(m,n,3);
       x=reshape(c(1,:,:),n,m);
       a(:,:,1)=x';
       x=reshape(c(2,:,:),n,m);
       a(:,:,2)=x';
       x=reshape(c(3,:,:),n,m);
       a(:,:,3)=x';
    endif
fclose (fid);
end

Il file deve essere di tipo ASCII, pgm o ppm. Nel primo caso in uscita è data una matrice $m\times n$ con i valori dei pixel dell'immagine; nel secondo caso è data una matrice $m\times n\times 3$ con i valori dei pixel nei tre canali del rosso, verde e blu. In tutte e due i casi il comando imagesc(A) visualizza il contenuto della matrice come immagine.

Naturalmente la presenza dei due cicli for annidati nella function ruota1 rallenta molto l'esecuzione del programma. È possibile però dare una versione vettorizzata di questa function. L'idea si basa su questa proprietà del linguaggio Octave:
se u è un vettore di m componenti e se v è un vettore di n componenti intere comprese tra 1 e m, allora w=u(v) è il vettore di n componenti date da w(i)=u(v(i)). Ad esempio, se u=[4 5 6 7] e v=[1 1 2 2 2 4] allora u(v) è il vettore [4 4 5 5 5 7]. La proprietà vale anche per matrici U e V se queste le interpretiamo come vettori ottenuti giustapponendo le colonne una dopo l'altra. Infatti, se U è $m\times n$ e V è $p\times q$ con elementi compresi tra 1 e $mn$, allora W=U(V) è la matrice $p\times q$ tale che W(i,j)=U(h,k), dove h e k si ottengono dalla decomposizione di V(i,j)=m(k-1)+h. Tale decomposizione mette in corrispondenza la coppia (h,k) con m(k-1)+h, quindi l'ordinamento indotto sulle coppie (h,k) è quello per colonne: (1,1), (2,1), ..., (m,1), (1,2),..., (m,n).
Ad esempio, vale
         11  44  77           4 9                44  99
U =   22  55  88    V = 9 1    U(V) = 99  11
         33  66  99           5 6                55  66

Legata a questa proprietà c'è l'istruzione vec che trasforma una matrice in un vettore. Infatti v=vec(A) dà un vettore v tale che v(q)=A(h,k) con q=m(k-1)+h, dove A è matrice m×m. Il vettore v si ottiene giustapponendo le colonne di A. L'operazione inversa la svolge il comando A=reshape(v,m,n).

Un possibile modo per svolgere la rotazione di una immagine senza usare cicli for procede con i seguenti passi. L'obiettivo è descrivere in modo compatto la trasformazione $(i',j') \to (i,j)$ dove $(i,j)$ è la generica coppia di indici del generico pixel dell'immagine di partenza e $(i',j')$ è la corrispondente coppia di indici del pixel dell'immagine trasformata.

-1- si costruisce una matrice V di dimensione $2\times mn$ che ha per colonne tutte le coppie $(i, j)$ con $i=1,\ldots,m$, $j=1,\ldots,n$. Come ordinamento, fissiamo prima l'indice di colonna $j$ e poi facciamo scorrere l'indice di riga $i$, cioè procediamo per colonne nello scandire le coordinate dell'immagine.
-2- Costruiamo la matrice W $2\times; mn$ che nella generica colonna $k$-esima ha gli indici $(i,j)$ dove la $k$-esima colonna di V ha gli indici $(i',j')$. nel caso della rotazione attorno a (i0,j0) di un angolo alfa, basta costruire la matrice R=[cos(alfa), sin(alfa);-sin(alfa) cos(alfa)] e calcolare W=[i0;j0]+R(V-[i0;j0]). Questo implementa in modo vettoriale le formule di rotazione, cioè abbiamo descritto la rotazione come trasformazione di $(i,j)$ in $(i',j')$ in modo compatto come V $\to$ W. Naturalmente poiché i nostri pixel hanno coordinate intere dobbiamo arrotondare il risultato di W alla parte intera. -3- Per realizzare la trasformazione dei pixel dell'immagine avendo a disposizione quella delle coordinate basta procedere così.   -3.1- si trasformano le coordinate bidimensionali racchiuse nelle colonne di W in coordinate monodimensionali con l'ordinamento per colonne, cioè si applica la trasformazione $(i,j) \to i+(j-1)m$. Per questo si costruisce il vettore Z=(W(2,:)-1)*m + W(1,:).
  -3.2- si dimensiona Z a matrice m×n come Z=reshape(W,m,n). La matrice Z avrà come elemento di posto $(i',j')$ il valore $i+(j-1)m$ dove ricordiamo che $(i',j')$ è il trasformato di $(i,j)$
  -3.3- si calcola infine Y=X(Z)

Se applichiamo il metodo così come l'abbiamo descritto è molto probabile che Octave ci segnali degli errori in esecuzione. Il problema è che dopo la rotazione alcune coordinate di pixel possono cadere fuori dal supporto dell'immagine, cioè i loro valori numerici possono non appartenere ai segmenti [1:m] per le righe e [1:n] per le colonne. In questo caso Octave ci segnalerebbe un errore. Occorre allora rimediare all'inconveniente modificando in modo opportuno il punto 3. Allora si procede così

-3.00- individuiamo i valori degli indici che cadono fuori del supporto [1,m]×[1,n]; per questo trasformiamo in 0 tutti i valori di W minori o uguali a 0, trasformiamo in $m+1$ gli indici della prima riga di W maggiori di $m$, e trasformiamo in $n+1$ gli indici della seconda riga di W maggiori di $n$;
-3.01- l'immagine X di dimensione m×n la bordiamo di zeri copiandola in una matrice XX di dimensioni $(m+2)\times(n+2)$, allo stesso tempo incrementiamo i valori di W di uno. In tal modo gli indici di riga o di colonna uguali a 1 individuano punti fuori del supporto e corrisponderanno a elementi (pixel) della cornice aggiunta all'immagine. Analogamente, indici di riga uguali a $m+2$ o di colonna uguali a $n+2$ individuano punti fuori dal supporto che corrisponderanno a elementi della cornice aggiunta all'immagine. Si pone X=XX

Il programma che si ottiene è il seguente

function Y = ruota2(X, p, ang)
% ruota l'immagine X attorno a p di un angolo ang
% in modo antiorario
m = size(X,1); n=size(X,2);
i0 = p(1); j0=p(2);
vi = vec([1:m]'*ones(1,n))';
vj = vec(ones(m,1)*[1:n])';
% trasforma
V = [vi-i0;vj-j0];
R = [cos(ang) sin(ang);-sin(ang) cos(ang)];
W = R*V + [i0;j0]*ones(1,n*m);
W = round(W);
% controllo delle coordinate fuori dal supporto
W = max(W,0);                              
W(1,:)=min(W(1,:),m+1);
W(2,:)=min(W(2,:),n+1);
W = W + 1;
XX = zeros(m + 2, n + 2);                  
XX(2:m+1, 2:n+1) = X;
Z = (m + 2)*(W(2,:)-1) + W(1,:);
ZZ = reshape(Z,m,n);                        
Y = XX(ZZ);
endfunction

La rotazione è una semplice trasformazione di coordinate. È possibile costruire trasformazioni arbitrarie, basta dare spazio alla fantasia. Una trasformazione interessante è quella che sposta un pixel in una direzione a caso di una quantita' a caso compresa tra tra 0 e 3. Un insieme di trasformazioni interessanti si ottiene usando funzioni di variabile complessa. Questo lo vediamo tra poco. Un'altro esempio interessante che richiede un po' di modellazione matematica è il caso di immagini anamorfiche ottenute mediante riflessioni su specchi non piani.

Esempio. Immagini anamorfiche.  Un modo interessante per applicare deformazioni ad una immagine assegnata consiste nel fare riflettere l'immagine originale su uno specchio cilindrico o su una sfera. Ad esempio, supponete di avere uno specchio cilindrico posto su un piano orizzontale $P$ e considerate un generico raggio che parte dal vostro occhio, colpisce la superficie del cilindro, viene riflesso e interseca il piano orizzontale $P$ in un punto $p$. Lo stesso raggio se non è riflesso, prosegue oltre il cilindro e interseca in un punto $q$ un piano obliquo $Q$ posto dietro il cilindro. Sapreste scrivere le relazioni che legano le coordinate di $p$ e di $q$ rispettivamente nel piano $P$ e nel piano $Q$? Se siete in grado di fare questo, potete modificare il programma ruota1 o il programma ruota2 in modo che data un'immagine generica genera una immagine anamorfica che può essere "riletta" fisicamente riflettendola in uno specchio cilindrico.

Esercizi un po' più semplici sono i seguenti:

Esercizio 1. Simulare come viene trasformata una fotografia se viene arrotolata attorno ad un semicilindro di altezza pari ad una delle sue dimensioni e i suoi punti vengono proiettati ortogonalmente su AB come in figura dove x è il generico punto dell'immagine e y quello dell'immagine trasformata.

Esercizio 2. Simulare la trasformazione inversa dell'esercizio 1. Cioè, data la foto nel piano generare la foto sul cilindro.

Esercizio 3. Con riferimento all'esercizio 1 simulare come viene trasformata una fotografia se il generico punto x dell'immagine originale viene trasformato in y come in figura.

Esercizio 4. Simulare la trasformazione inversa dell'esercizio 3. Cioè, data la foto blu nel piano generare la foto sul cilindro.

Esercizio 5. Data una immagine $m\times n$ e preso il pixel centrale $(i_0,j_0)$ si deformi l'immagine col cambio di coordinate $(i,j)\to(i',j')$ dove $i'=i_0+m((i-i_0)/m)^3$, $j'=j_0+n((j-j_0)/n)^3$.

Esercizio 6. Data una immagine $m\times n$ e preso il pixel centrale $(i_0,j_0)$ si deformi l'immagine col cambio di coordinate inverso a quello dell'esercizio 5.

Esercizio 7. data una immagine $m\times n$ e preso il pixel centrale $(i_0,j_0)$ si deformi l'immagine col cambio di coordinate $(i,j)\to(i',j')$ dove $(i',j')^T=(i_0,j_0)^T + A(i-i_0,j-j_0)^T$ dove $A$ è la matrice di elementi $a_{i,j}$ per $i,j=1,2$ di valore assoluto scelto a caso tra zero e 1.

Esercizio 8. Data una immagine $m\times n$ e preso il pixel centrale $(i_0,j_0)$ si deformi l'immagine col cambio di coordinate $(i,j)\to(i',j')$ dove $i'=i_0+m\sqrt 2\cos((i-i_0)/m))\sin((j-j_0)/n)$, $j'=j_0+n*\cos((j-j_0)/n))$.

Compito: Svolgere uno degli 8 esercizi precedenti.

2.1-Manipolazioni geometriche con funzioni di variabile complessa.
Interessanti trasformazioni si ottengono utilizzando funzioni di variabile complessa. Data un'immagine costituita dall'insieme dei pixel $a(i,j)$, per $i=1,\ldots,m$, $j=1,\ldots,n$ associamo alla coppia $(i,j)$ un numero complesso $z=z(i,j)$, ad esempio $z=(j-j_0)h + {\bf i}(i-i_0)h$ dove abbiamo denotato con {\bf i} l'unità immaginaria tale che ${\bf i}^2=-1$, e dove abbiamo scelto $i_0,j_0$ e $h$ a nostro piacere. Oltre all'applicazione $(i,j)\to(i,j)$ consideriamo l'applicazione "inversa" $z(i,j)\to(i,j)$ tale che $j$ è la parte intera di Re$(z)/h +j_0$, mentre $i$ è la parte intera di Im$(z)/h+i_0$, dove abbiamo indicato con Re(.) e Im(.) la parte reale e la parte immaginaria di un numero complesso.
Consideriamo poi una funzione di variabile complessa $y=f(z)$, ad esempio $f(z)=z^2/|z|$, e costruiamo questa trasformazione tra coppie di interi $(i',j')$ e $(i,j)$
$(i,j)\to z(i,j)$, $w=f(z)$, $w\to(i',j')$
Costruiamo l'immagine che nel pixel di coordinate $(i,j)$ ha il valore $a(i',j')$ se $(i',j')$ appartiene a $[1,m]\times[1,n]$, ha il valore 0 altrimenti. Come è fatta l'immagine deformata in questo modo?
Cosa accade con semplici funzioni quali $f(z)=zt$, se $t$ è un numero complesso di modulo 1, oppure se $t$ è un numero reale positivo?
Cosa accade con funzioni più complesse quali $f(z)=z(z/|z|)^k$, per $k$ intero? Oppure con $f(z)=z-(z^3-1)/(2z^2)$?

Questa e una traccia di programma Octave per deformare immagini

function Y = complextransform(X)
   m = size(X)(1);
   n = size(X)(2);
   h = 2/max(m,n);
   Y = zeros(m,n);
   i0 = round(m/2); j0 = round(n/2);
% scandisco supporto della foto trasformata
   for ip = 1 : m
      for jp = 1 : n
% calcolo il numero complesso corrispondente
         z = (jp-j0)*h + I*(ip-i0)*h;
% trasformo all'indietro
         if abs(z) != 0
            w=z*(z/abs(z))^2;
         else
            w = 0;
         endif
% calcolo le coordinate del pixel corrispondente a w
         i = round(i0+imag(w)/h);
         j = round(j0+real(w)/h);
% assegno il colore
         if(1<=i&& i<=m && 1 <=j && j<=n)
            Y(ip,jp) = X(i,j);
         else
            Y(ip,jp)=0;
         endif
      endfor
   endfor
endfunction

Ecco alcuni esempi ottenuti con varie funzioni

Di seguito si riporta una function per costruire immagini ottenute con trasformazioni di variabile complessa evitando cicli for. La function è ottenuta modificando leggermente la function ruota2.

function Y = complextransform2(X, p)
% trasforma l'immagine X mediante funzione di variabile
% complessa
% X: immagine
% p=[i0,j0]: coordinate del pixel in cui e' messa l'origine
% nel piano complesso
% il programma e' un adattamento della function ruota2
    m = size(X,1); n=size(X,2);
    i0 = p(1); j0=p(2);
    vi = vec([1:m]'*ones(1,n))';
    vj = vec(ones(m,1)*[1:n])';

    %%%%%%% trasforma
    V = [vi-i0;vj-j0];
    z=V(2,:)+I*V(1,:);
    z=z.*(z./(abs(z)+1.0e-16)).^2; % funzione
    W=zeros(2,m*n);
    W(2,:)=real(z);W(1,:)=imag(z);
    W = round(W) + [i0;j0]*ones(1,n*m);
    %%%%%%%%

    % controllo delle coordinate fuori dal supporto
    W = max(W,0);
    W(1,:)=min(W(1,:),m+1);
    W(2,:)=min(W(2,:),n+1);
    W = W + 1;
    XX = zeros(m + 2, n + 2);
    XX(2:m+1, 2:n+1) = X;
    Z = (m + 2)*(W(2,:)-1) + W(1,:);
    ZZ = reshape(Z,m,n);
    Y = XX(ZZ);
endfunction

Esercizio 1'. Simulare l'azione di una lente di ingrandimento trasformando una immagine in modo da ingrandirne una parte con continuità, e quindi senza strappi, lasciando la parte rimanente inalterata.

Le seguenti immagini sono state create da studenti del corso dell'aa. 2008-2009.

Esercizio 2'. Realizzare la rotazione di una immagine usando una opportuna funzione di variabile complessa.

Esercizio 3'. Realizzare la trasformazione di una immagine usando la funzione esponenziale e la funzione logaritmo.

Esercizio 4'. Realizzare la trasformazione di una immagine usando la funzione seno e la funzione coseno.

Esercizio 5'. Realizzare la trasformazione di una immagine usando la trasformata di Cayley $z \to (1-z)/(1+z)$.

Esercizio 6'. Realizzare la trasformazione di una immagine usando la funzione $z\to (z+1/z)/2$.

Esercizio 7'. Realizzare la trasformazione di una immagine usando come trasformazione inversa separatamente una, due e tre iterazioni del metodo di Newton applicato a $x^3-1$.

Esercizio 8'. Realizzare la trasformazione di una immagine usando come trasformazione inversa separatamente una, due e tre iterazioni del metodo di Newton applicato a $x^4-1$.

3-Decomposizione spettrale, filtraggio e compressione.

Sia $n$ un intero positivo che supponiamo per semplicità pari, cioè $n=2m$. Consideriamo i vettori $c^{(j)}$, $j=0,1,\ldots,m$, $s^{(j)}$, $j=1,\ldots,m-1$, di $n$ componenti definiti da $c^{(j)}_i=\cos(2ij\pi/n)$, $s^{(j)}_i=\sin(2ij\pi/n)$, $i=0,\ldots,n-1$. Ciascuno di questi vettori si ottiene calcolando rispettivamente le funzioni $\cos(jx)$ e $\sin(jx)$ nei punti $x_i=2i\pi/n$, $i=0,1,\ldots,n-1$. Come dicono gli ingegneri i vettori $s^{(j)}$ e $c^{(j)}$ sono i campionamenti delle funzioni $\cos(jx)$ e $\sin(jx)$ nei nodi $x_i$. Quindi i vettori $c^{(j)}$ e $s^{(j)}$ rappresentano in termini discreti le funzioni $cos(jx)$ e $sin(jx)$ che hanno periodo $2\pi/j$ e quindi frequenza $j/2\pi$.

Qui sotto si riportano graficamente i vettori $s^{(1)}$, $s^{(2)}$, $s^{(3)}$, $s^{(4)}$.

Si può verificare che gli $n$ vettori così costruiti sono linearmente indipendenti per cui ogni vettore $v=(v_i)$ di $n$ componenti può essere rappresentato nella base costituita da questi vettori speciali. Vale cioè

$v=a_0c^{((0)}+ (a_1c^{(1)} + b_1s^{(1)}) + (a_2c^{(2)} + b_2s^{(2)}) + \cdots + (a_{m-1}c^{(m-1)} + b_{m-1}s^{(m-1)}) + a_mc^{(m)}$

Nel caso di $n$ dispari, cioè $n=2m-1$ i vettori $c^{(j)}$, $i=0,...,m-1$, $s^{(j)}$, $j=1,\ldots,m$, sono ancora linearmente indipendenti e vale una espressione analoga alla precedente, cioè

$v=a_0c^{(0)} + (a_1c^{(1)} + b_1s^{(1)}) + (a_2c^{(2)} + b_2s^{(2)}) + \cdots + (a_{m-1}c^{(m-1)} + b_{m-1}s^{(m-1)}) $

I coefficienti $a_i$ e $b_i$ possono essere calcolati, a partire dalle componenti di $v$ mediante l'algoritmo FFT (Fast Fourier Transform) della trasformata veloce discreta di Fourier del quale esistono numerose implementazioni in diversi linguaggi di programmazione. Infatti, se $v$ è reale e $u=$fft$(v)$, cioè

$ u_i=(1/n)\sum_j(\cos(2\pi ij/n)+{\bf i}\sin(2\pi ij/n))v_j, $

con $\bf i$ unità immaginaria, vale la seguente proprietà

se $n=2m$ allora $u=[u_0, u_2, \ldots , u_m, u_{m+1}, \hat u_m, \ldots, \hat u_1]$,
se $n=2m-1$ allora $u=[u_0, u_1, \ldots, u_m, \hat u_m, \ldots, \hat u_1]$,

dove $u_0, u_{m-1}$ sono reali e $\hat u_i$ indica il coniugato del numero complesso $u_i$, inoltre

$a_i=2$Re$(u_i)$
$b_i=-2$Im$(u_i)$

La rappresentazione di un vettore nella base speciale di seni e di coseni permette di considerare un vettore generico come somma di vettori "oscillanti" con frequenze multiple intere della frequenza $1/(2\pi) e di ampiezze date da

$A_j=(a_j^2+b_j^2)^{1/2}=2|u_j|$.

Infatti, mediante note identità trigonometriche, la rappresentazione data si può scrivere come \[ v_i=a_0+A_1 \cos(i \frac{2\pi}n + B_1) + A_2 \cos(2i \frac{2\pi}n + B_2) + A_3 \cos(3i \frac{2\pi}n + B_3) + \cdots + A_{m-1} \cos((m-1)i \frac{2\pi}n + B_{m-1}) + A_m\cos(m i \frac{2\pi}n+B_m) \]

Questa trasformazione è molto usata dagli ingegneri per filtrare segnali. Infatti la decomposizione in termini di funzioni trigonometriche elementari (decomposizione spettrale) ci permette di conoscere le ampiezze $A_j$ e le fasi $B_j$ con cui ogni singola frequenza elementare compare nel segnale. Con questa informazione possiamo fare manipolazioni di segnali molto efficaci, quali amplificare o ridurre le tonalità acute o gravi di un suono rappresentato in forma digitale mediante il vettore $v$.

Si veda il sito http://www.westga.edu/~jhasbun/osp/Fourier.htm per un grazioso strumento legato a queste rappresentazioni. Ad esempio si può costruire un nuovo vettore $w$ ottenuto amplificando le componenti in "bassa frequenza" sostituendo ad esempio i valori $A_i$ con $2A_i$ se $i$ è minore di $n/4$.  Analogamente possiamo amplificare o attenuare le alte o le medie frequenze e trasformare il vettore originale in diversi modi. Se il vettore rappresenta un segnale acustico, ad esempio un brano di musica, le operazioni descritte hanno l'effetto analogo a quello che si ottiene regolando i toni in un impianto hifi. Questo tipo di manipolazione numerica è esattamente quella che svolgono certe applicazioni che riproducono musica digitale su di un pc.

Caso $n=16$ [0 1 2 3 4 5 6 7 8 7 6 5 4 3 2 1]
Caso $n=17$ [0 1 2 3 4 5 6 7 8 8 7 6 5 4 3 2 1]

Se ad esempio volessimo rimuovere da un vettore $v$ di 16 componenti le componenti in frequenza relative alle frequenze 5, 6, 7, 8, dovremmo operare nel seguente modo:

-1- si calcola $u=$fft$(v)$
-2- si considera il vettore filtro $f=[1 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1]$
-3- si moltiplica componente a componente $u$ con $f$ e si ottiene $z$ (nella sintassi di Octave z = u.*f)
-4- si antitrasforma $z$ e si ottiene $w = $ifft$(z)$

dove ifft è la trasformata discreta inversa di Fourier. Il vettore $w$ fornisce il segnale filtrato. Se ad esempio volessimo ridurre di un fattore 1/2 l'ampiezza delle componenti in frequenza 5,6, e annullare le componenti in frequenza 7 e 8 il vettore filtro sarebbe

f=[1 1 1 1 1 1/2 1/2 0 0 0 1/2 1/2 1 1 1 1]

Octave ha la funzione y=fft(x) che fornisce la trasformata discreta di Fourier y del vettore x. Inoltre esiste la funzione x=ifft(y) che fornisce la trasformata discreta inversa.

Diamo ora un esempio di filtraggio di un segnale. Sia $n=512$ il numero di punti di campionamento in cui si divide l'intervallo $[0,2\pi]$. Poniamo h=2pi/n e x=[0:h:2*pi-h]. Scegliamo come funzione

$y=\sin(x)^2+0.1\cos(4x^2-x+1)+0.05\sin(100x)$

che ha grafico

Quindi, usando Octave scriviamo

n=512; h=2*pi/n; x=[0:h:2*pi-h];
y=sin(x).^2 + 0.1*coz(4*x.^2-x+1) + 0.05*sin(100*x);
plot(y);

Il grafico che otteniamo ha delle oscillazioni molto fitte "in alta frequenza". Per rinuoverle procediamo nel modo seguente. Si crea un filtro che azzera le componenti in frequenza più alte come segue

f=ones(1,n);
m=n/2+1;
f(m-200:m+200)=0;

e adesso filtriamo

w=ifft(fft(y).*f);
w=real(w);
plot(w);

e otteniamo il grafico

Nel caso delle immagini si possono fare filtraggi analoghi agendo separatamente sui vettori colonna e sui vettori riga di un'immagine. Si supponga di avere una matrice $A$ $m\times n$ che contiene una immagine. Per rimuovere le alte frequenze (dettagli minuscoli) in $A$ basta calcolare la trasformata discreta di Fourier delle righe e la trasformata discreta delle colonne di $A$, moltiplicare ciascuna colonna del risultato componente a componente con un vettore filtro, fare la stessa cosa sulle righe e antitrasformare.

Octave ha le funzioni fft2 e ifft2 che svolgono la trasformata discreta diretta e inversa delle righe e delle colonne di una matrice. Una function di filtraggio di immagini in Octave, che rimuove le frequenze alte dall'immagine è la seguente.

function B=filtra(A)
   m = size(A)(1); n = size(A)(2);
% calcolo fft di righe e colonne
   B = fft2(A);
% filtro le righe
   k = floor((m-1)/2)
   v = ones(1,k);
   v(k-70:k) = 0;
   if(mod(m,2) == 0) % caso m pari: [0 1 2 3 4 3 2 1]
      f1 = [1,v,0,v(k:-1:1)];    else % caso m dispari: [0 1 2 3 3 2 1]
      f1 = [1,v,v(k:-1:1)];
   endif
% filtro per le colonne
   k = floor((n-1)/2)
   v = ones(1,k);
   v(k-70:k) = 0;
   if(mod(n,2) == 0) % caso n pari: [0 1 2 3 4 3 2 1]
      f2 = [1,v,0,v(k:-1:1)];    else % caso n dispari: [0 1 2 3 3 2 1]
      f2 = [1,v,v(k:-1:1)];
   endif
% filtro e antitrasformo
   B = ifft2(diag(f1)*B*diag(f2));
   B = real(B); % tolgo eventuale roundoff immaginario
   B = max(B,0);% riporto i valori nel range 0--255
   B = min(B,255);    B = round(B);
endfunction

Si noti la simmetria di un filtro data dal fatto che il vettore ottenuto rimuovendo la prima componente di $f$ è simmetrico rispetto al centro.

Si può osservare che se $v$ è reale allora il vettore $u$ è tale che $u_0$ e $u_{n/2+1}$ sono reali mentre $u_j$ è il complesso coniugato di $u_{n-j}$. Per cui, affinché un filtro $f$ mantenga la realtà del segnale filtrato, occorre che $f$ sia ''simmetrico'' nel senso che $f_j=f_{n-j}$, $j=1,\ldots,n/2-1$. Basta quindi definire il filtro in $f_0,\ldots,f_m$.

S=2*pi*[0:m-1]'*(250*ones(1,n)+50*rand(1,n))/m;
T=[0:n-1]'*(250*ones(1,m)+50*rand(1,m))*2*pi/m;
R=sin(S)+sin(T)';
X=A+R;

che genera frequenze a caso comprese tra $250/(2\pi)$ e $255/(2\pi)$ sia sulle righe che sulle colonne.

Foto originale

Foto con rumore

Foto filtrata

Ecco un esempio di immagine ottenuta a partire dalla fotografia dei cammelli amplificando le alte frequenze. A sinistra l'immagine filtrata, a destra quella originale. In questo caso, essendo l'immagine a colori, si è fatto il filtraggio sulle tre componenti R,G,B. Si puό vedere il maggior dettaglio nei particolari delle foglie e nei tronchi delle palme.

Un filtro ''passa alto'' è dato da

$f_j=1-\cos(2\pi j/n)$, $j=0,\ldots,n/2$

infatti, dal grafico della funzione $1-\cos x$

si vede che il filtro riduce l'ampiezza delle componenti in bassa frequenza

Mentre un filtro "passa basso" è

$f_j=1+\cos(2\pi j/n)$, $j=0,\ldots,n/2$

Come agisce invece il filtro seguente?

$f_j=1-\cos(3 \pi/2 + 2 \pi j/n)$, $j=0,\ldots,n/2$

Si osservi che il grafico della funzione associata al filtro l'abbiamo tracciato sull'intervallo $[0,\pi]$. Infatti il numero di componenti di $f$ è $n/2$ se $n$ è pari e $(n-1)/2$ se $n$ è dispari.

Filtri bassa basso e passa alto si possono più semplicemente costruire mediante combinazioni lineari di pixel evitando l'uso della fft.

Ad esempio una trasformazione che realizza un filtro passa basso e trasforma l'immagine $A$ nell'immagine $B$ è data da

$b_{i,j} = (a_{i,j} + a_{i+1,j} + a_{i-1,j} + a_{i,j+1} + a_{i,j-1})/5$

Un filtro passa alto è

$b_{i,j} = 4a_{i,j} - a_{i+1,j} - a_{i-1,j} - a_{i,j+1} - a_{i,j-1}$

Esercizio 1. Si implementino i filtri passa basso e passa alto mediante trasformata di Fourier discreta.

Esercizio 2. Si implementi il filtro dato da $1-\cos(3\pi/2 + 2\pi j/n)$.

Esercizio 3. Si implementi il filtro dato da $2-\cos(2\pi j/n)$.

Esercizio 4. Si implementi il filtro ottenuto prendendo la potenza $k$-esima, $k=2,3$ dei filtri degli esercizi 1 e 2.

Esercizio 5. Si implementino i filtri passa alto e passa basso che non usano la trasformata discreta di Fourier.

Esercizio 6. Si implementi il filtro

$b_{i,j} = 4a_{i,j} - a_{i+1,j} - a_{i-1,j} - a_{i,j+1} - a_{i,j-1}$

Esercizio 7. Si implementi il filtro

$b_{i,j} = 5a_{i,j} - a_{i+1,j} - a_{i-1,j} - a_{i,j+1} - a_{i,j-1}$

La stessa tecnica di filtraggio può essere utilizzata per comprimere un'immagine. Questo avviene memorizzando solamente i valori delle ampiezze che corrispondono alle frequenze più basse e si basa sul fatto che generalmente le "alte frequenze", cioè la ricchezza di dettagli minuscoli, non sono presenti in tutte le parti di una immagine. Quindi decomponendo un'immagine in porzioni più piccole ad esempio $8\times 8$ pixel, e calcolando la rappresentazione spettrale di queste sotto immagini, è possibile rappresentarle in modo abbastanza fedele memorizzando solo le basse frequenze nel caso in cui le alte abbiano valori in ampiezza trascurabili. Questa è l'idea alla base della compressione JPG.